Шугамын градиентийг хэрхэн олох вэ: 9 алхам (зурагтай)

2024 Зохиолч: Jason Gerald | [email protected]. Хамгийн сүүлд өөрчлөгдсөн: 2024-01-19 22:13

Алгебр 1, Геометр, Алгебра 2 -ийг ашиглаж байгаа эсэхээс үл хамааран математикийн аль ч хэсэгт мөрүүдийг олж болно. Хэрэв та шулууны градиентийг хэрхэн олохоо мэддэг бол, жишээ нь хоёр шугам зэрэгцээ эсвэл перпендикуляр байвал олон зүйл тодорхой болно., огтлолцох болон бусад олон ойлголтууд. Шугамын градиентийг олох нь үнэндээ маш хялбар байдаг. Шугамын градиентийг хэрхэн олох талаар сурахад ашиглаж болох зарим хялбар алхмуудыг үргэлжлүүлэн уншаарай.

Алхам

2 -ийн 1 -р арга: Градиент томъёо

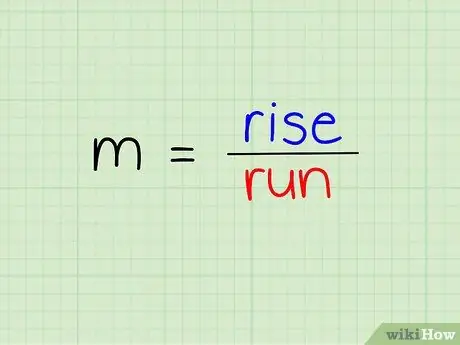
Алхам 1. Градиент томъёог ойлгох

Градиентийг босоо байдлаар хэвтээ байдлаар хуваана.

2 -ийн 2 -р арга: Градиент олох

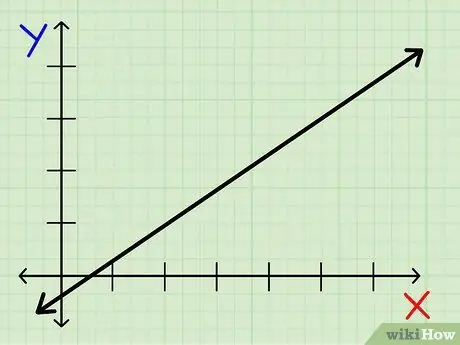
Алхам 1. Градиентийг олохыг хүсч буй шугамаа олоорой

Шугам шулуун байгаа эсэхийг шалгаарай. Та шулуун биш шулууны градиентийг олж чадахгүй.

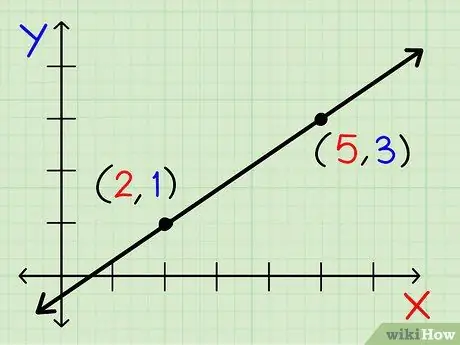
Алхам 2. Шугам дамжин өнгөрөх дурын хоёр координатыг сонгоно уу

Координат нь бичсэн x ба y цэгүүд (x, y) юм. Аль цэгийг сонгох нь хамаагүй, оноо нь ялгаатай бөгөөд нэг мөрөнд хэвтэж байвал л болно.

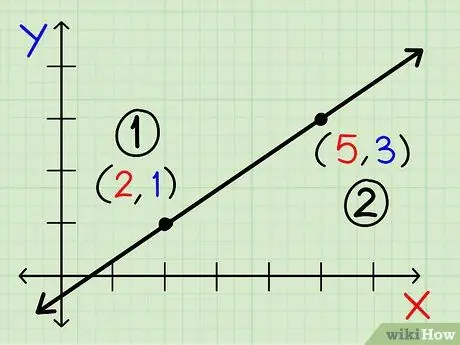
Алхам 3. Өөрийн тэгшитгэл дэх давамгайлах координатын цэгийг сонгоно уу

Тооцооллын явцад утга нь үргэлж ижил байх тохиолдолд аль цэгийг сонгох нь хамаагүй. Зонхилох координат нь x ₁ ба у ₁. Нөгөө координат нь x ₂ ба у ₂.

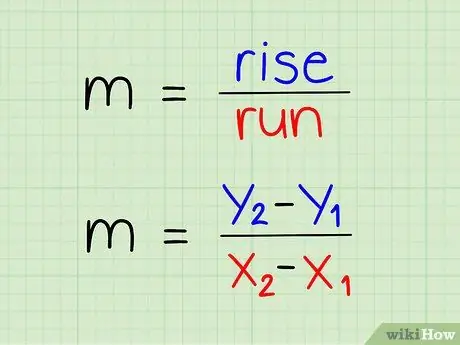
Алхам 4. Дээрх у координат, доорх x координаттай тэгшитгэлээ бичээрэй

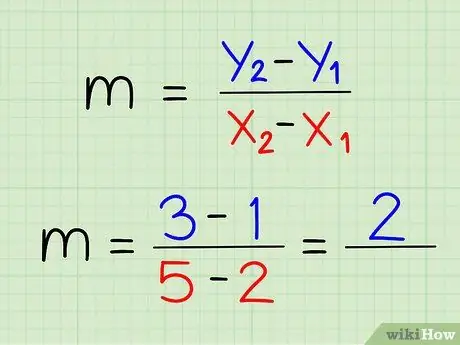
Алхам 5. Хоёр у-координатыг бие биенээсээ хас

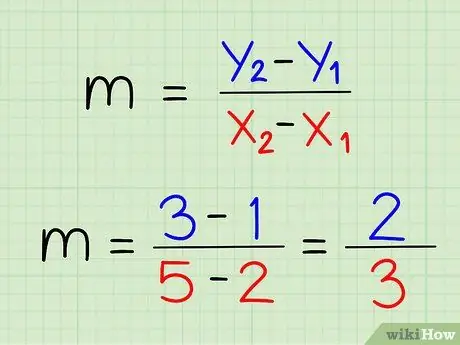
Алхам 6. Хоёр x координатыг бие биенээсээ хас

Алхам 7. y координатыг хасах үр дүнг x координатыг хасах үр дүнд хуваана

Хэрэв дугаарыг хялбарчлах боломжтой бол хялбаршуулаарай.

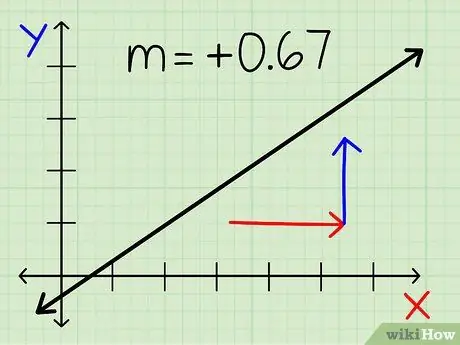
Алхам 8. Таны хариулт утга учиртай эсэхийг дахин шалгана уу

• Зүүнээс баруун тийш чиглэсэн мөр нь бутархай байсан ч үргэлж эерэг байдаг.
• Зүүнээс баруун тийш уруудах шугам нь бутархай ч гэсэн үргэлж сөрөг байдаг.

Жишээ

1. Мэдэгдэж байгаа: AB шугам.
2. Координат: A - (-2, 0) B - (0, -2)
3. (y₂-y₁): -2-0 = -2; Босоо = -2
4. (x₂-x₁): 0-(-2) = 2; Хэвтээ = 2

5. AB шугамын градиент = (Босоо/хэвтээ) = -1.

   Зөвлөмж

   • Хэрэв та зонхилох цэгийнхээ координатыг аль хэдийн сонгосон бол бусад координатаар сольж болохгүй, эс тэгвээс таны хариулт буруу болно.
   • Та m-ийг Шугамын томъёоноос олох болно: y = mx+b, энд y нь аливаа цэгийн y-координат, m нь градиент, x нь аль ч цэгийн y-координаттай харгалзах x координат, ба b бол y-огтлолцол юм.
   • Та сургуулийнхаа сурах бичгийг үзэх эсвэл багшаасаа асууж болно.